Experiment With Mixup

I wrote an app to classify an object using transfer learning, and the model was trained on CIFAR-10 dataset, all by myself.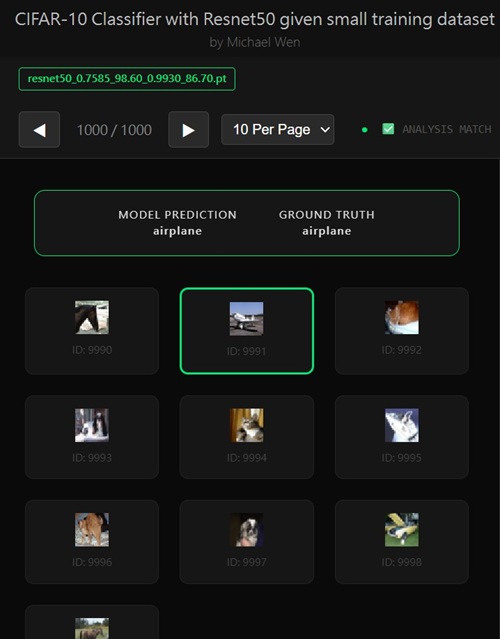

Why MixUp Makes Training Metrics Look Chaotic — and Why That’s a Good Sign

When MixUp is introduced into a two-stage fine-tuning setup, the first thing most readers notice is that the training metrics suddenly look unstable (look below).

Training accuracy jumps dramatically from epoch to epoch (look below).
Training loss oscillates instead of decreasing smoothly (look below).
At the same time, validation loss steadily decreases and validation accuracy continues to rise (look below).

At first glance, this feels counterintuitive — almost as if training has become unstable.
In reality, this behavior is exactly what a correctly implemented MixUp pipeline is expected to produce.

To understand why, we need to revisit what MixUp actually changes in the learning objective and how that affects the meaning of standard metrics.

What MixUp Changes at a Fundamental Level

MixUp modifies the training distribution itself.

Instead of learning from samples of the form:

(image A, class A) 

The model is trained on synthetic samples:

λ · image A + (1 − λ) · image B 
λ · label A + (1 − λ) · label B 

where λ is sampled from a Beta distribution (α = 0.2 in my setup).

This single change has deep implications for how we should interpret training accuracy, training loss, and their relationship to validation metrics.

1. Why Training Accuracy Jumps Up and Down by Large Amounts

Training accuracy becomes semantically incorrect under MixUp

Training accuracy is still computed using hard labels:

 argmax(prediction) == original_class 

However, MixUp trains the model against soft targets that intentionally contain ambiguity.

Example:

Target: 0.7 cat + 0.3 dog 
Prediction: 0.55 dog + 0.45 cat 

From a MixUp loss perspective, this is a reasonable prediction.
From an accuracy perspective, it is counted as wrong.

Because each mini-batch contains randomly mixed pairs with different λ values, the apparent training accuracy becomes highly noisy.

• Accuracy no longer reflects learning progress
• Accuracy is dominated by random pairing and interpolation ratios
• Large epoch-to-epoch swings are expected

This explains sudden jumps such as:

23.5% → 8.8% → 32.8% → 8.7% 

Nothing is unstable — the metric is simply misaligned with the training objective.

2. Why Training Loss Also Jumps Up and Down

MixUp intentionally injects optimization noise

Under MixUp, the loss surface becomes more complex:

• The model must predict calibrated probability distributions
• Overconfident predictions are penalized
• Each batch represents a different synthetic task

Unlike standard cross-entropy training, there is no single “correct” class to collapse toward.

As a result:

• Loss values respond sensitively to small logit shifts
• Batch composition changes dominate short-term loss behavior
• Smooth monotonic loss curves are no longer expected

The oscillations you observe (logs provided below) are a feature, not a bug — they are the price paid for enforcing smoother decision boundaries.

3. Why Validation Loss Goes Down Despite Chaotic Training Metrics

Validation evaluates the representation, not the training objective

Validation is performed on:

• Clean images
• True, unmixed labels
• A fixed, stationary data distribution

MixUp never directly optimizes validation performance.
Instead, it reshapes the learned feature space indirectly.

What the model actually learns

• Smoother transitions between classes
• Wider, flatter decision boundaries
• Reduced reliance on brittle, high-frequency cues

These properties do not immediately improve training accuracy — but they dramatically improve generalization.

This is why validation loss decreases steadily even when training loss appears unstable.

4. Why Validation Accuracy Goes Up Despite Erratic Training Accuracy

Generalization improves even when memorization is suppressed

MixUp prevents the network from forming overly sharp decision boundaries that perfectly separate the training set but fail on unseen data.

Instead, the model is forced to respect this constraint:

Similar inputs must produce similar outputs 

This directly improves robustness on real validation images.

• Less overfitting
• Better probability calibration
• Improved class separation under distribution shift

As a result, validation accuracy increases steadily toward ~86–87%, even though training accuracy remains noisy and misleading.

Final Takeaway: This Is Data-Driven Progress, Not Random Luck

The most important conclusion is this:

• The strange-looking training metrics are mathematically expected
• The validation improvements are consistent and repeatable
• The behavior aligns with known properties of MixUp regularization

When erratic training metrics coexist with improving validation loss and accuracy, it is a strong signal that:

Regularization is working exactly as intended 

This is not intuition or guesswork.
It is inference based on observed learning dynamics, loss behavior, and generalization theory.

In short:

You are no longer optimizing to look good on the training set.
You are shaping the model to perform better on unseen data — and the validation results confirm the decision.

Digging Deeper - How the Cost Function Changes When MixUp Is Added

MixUp does not merely add noise to training data — it fundamentally changes the cost function the model is optimizing.

To fully understand why training behavior looks different under MixUp, we need to walk step by step through how the loss is constructed, how gradients are computed, and what the model is truly being rewarded for.

Baseline: Cost Function Without MixUp

Assume a standard classification setup with cross-entropy loss.

For a single training example with true class y and model logits z:

p = softmax(z)
Loss = -log(p[y])

Key properties of this objective:

• The target label is one-hot
• Only one class is considered correct
• The loss pushes probability mass aggressively toward a single class

If the model predicts the correct class with high confidence, the loss approaches zero.
This encourages sharp decision boundaries and fast memorization — especially on small datasets.

What MixUp Changes Conceptually

With MixUp, we no longer train on a single labeled example.

Instead, two samples are combined:

x̃ = λ · x₁ + (1 − λ) · x₂
ỹ = λ · y₁ + (1 − λ) · y₂

where:

• x₁, x₂ are input images
• y₁, y₂ are one-hot labels
• λ ∈ (0, 1) is sampled from Beta(α, α)

The target label is now a probability distribution, not a single class.

Cost Function With MixUp

The cross-entropy loss is computed against the soft target ỹ:

Loss = - Σᵢ ỹᵢ · log(pᵢ)

Where ỹᵢ is actual labels and pᵢ is model's predicted probabilities.

Substituting the MixUp target:

Loss = - [ λ · log(p[y₁]) + (1 − λ) · log(p[y₂]) ]

This single equation explains most of MixUp’s training behavior.

Explanation of Each Term in the MixUp Loss Formula

We start from the MixUp cross-entropy loss:

Loss = - Σᵢ ỹᵢ · log(pᵢ)

and its expanded form for two mixed samples:

Loss = - [ λ · log(p[y₁]) + (1 − λ) · log(p[y₂]) ]

Below is a precise, term-by-term explanation so there is zero ambiguity about what each symbol means and why it exists.

pᵢ — Model-Predicted Probability for Class i

pᵢ = softmax(z)ᵢ

• pᵢ is the model’s predicted probability for class i
• It comes from applying softmax to the model’s logits
• All pᵢ values sum to 1

Example:

p = [0.55 (cat), 0.45 (dog)]

Here:

• p₀ = 0.55
• p₁ = 0.45

ỹᵢ — Soft (Mixed) Target Probability for Class i

ỹ = λ · y₁ + (1 − λ) · y₂

• ỹᵢ is the target probability assigned to class i
• Unlike standard training, ỹ is not one-hot
• It encodes how much each original label contributes to the mixed sample

Example:

y₁ = [1, 0]   (cat)
y₂ = [0, 1]   (dog)
λ = 0.7

ỹ = [0.7, 0.3]

So:

• ỹ₀ = 0.7
• ỹ₁ = 0.3

Σᵢ — Sum Over All Classes

Σᵢ ỹᵢ · log(pᵢ)

• The loss considers every class, not just one
• Each class contributes proportionally to its target weight ỹᵢ
• This is why MixUp produces smoother gradients

In practice, only classes with non-zero ỹᵢ matter.

p[y₁] — Predicted Probability of the First Sample’s True Class

p[y₁]

• y₁ is the class index of the first original sample
• p[y₁] means “the model’s predicted probability for class y₁”

Example:

y₁ = cat
p[cat] = 0.55

This term measures how well the model predicts the first component of the MixUp pair.

p[y₂] — Predicted Probability of the Second Sample’s True Class

p[y₂]

• y₂ is the class index of the second original sample
• p[y₂] is the probability assigned to that class

Example:

y₂ = dog
p[dog] = 0.45

Why the Loss Splits into Two Terms

Substituting the soft target into cross-entropy:

Loss = - Σᵢ ỹᵢ · log(pᵢ)

Since only y₁ and y₂ have non-zero weights:

Loss = - [ λ · log(p[y₁]) + (1 − λ) · log(p[y₂]) ]

Interpretation:

• The model is rewarded for predicting both classes correctly
• The reward is proportional to how much each sample contributes
• No single class is ever “100% correct”

Intuition Summary

• pᵢ: what the model believes
• ỹᵢ: what the model should believe
• p[y₁]: confidence in the first mixed label
• p[y₂]: confidence in the second mixed label

The loss simply measures how well these beliefs align — but under a deliberately softened, uncertainty-aware target.

Key Insight

Once you understand these terms, it becomes clear why MixUp:

• Destroys the meaning of training accuracy
• Makes loss noisier but gradients healthier
• Improves validation accuracy despite “ugly” training logs

Nothing is broken — the objective itself has changed.

Concrete Numerical Example

Assume:

• Class A = cat
• Class B = dog
• λ = 0.7

Target distribution:

ỹ = [0.7 (cat), 0.3 (dog)]

Model prediction:

p = [0.55 (cat), 0.45 (dog)]

Loss calculation:

Loss = - [0.7 · log(0.55) + 0.3 · log(0.45)]
     ≈ 0.77

Compare this to standard training:

• If cat were the only correct class → loss = -log(0.55) ≈ 0.60
• MixUp penalizes overconfidence and rewards balance

Why Training Loss Becomes Noisy

Each mini-batch introduces new random pairs and new λ values.

As a result:

• The target distribution changes every iteration
• The optimal prediction is no longer a one-hot vector
• Small logit changes cause large loss variations

Loss noise is therefore a direct consequence of optimizing a richer objective, not unstable learning.

Effect on Gradients

Without MixUp, the gradient pushes hard toward one class:

∂Loss/∂zᵢ = pᵢ − 1(y = i)

With MixUp:

∂Loss/∂zᵢ = pᵢ − ỹᵢ

This means:

• Gradients are smaller and smoother
• No class is ever pushed to probability 1.0
• Learning favors calibrated probabilities

This is why MixUp improves generalization but slows memorization.

Why Training Accuracy Becomes Meaningless

Accuracy is computed as:

argmax(p) == argmax(y)

But under MixUp:

• ỹ does not have a single correct class
• Predictions near the optimal distribution can still be marked “wrong”

This disconnect explains why training accuracy oscillates wildly while validation accuracy improves.

Relationship to Label Smoothing

MixUp generalizes label smoothing:

• Label smoothing distributes mass across all classes
• MixUp distributes mass across specific semantic classes

Both modify the loss function to discourage overconfidence, but MixUp also reshapes the input space.

Why This Cost Function Improves Generalization

Optimizing this loss enforces a powerful inductive bias:

If two inputs are similar, their predictions should interpolate smoothly

This produces:

• Smoother decision boundaries
• Reduced sensitivity to noise
• Better behavior under distribution shift

These properties are invisible in training accuracy but clearly reflected in validation performance.

Final Takeaway

When MixUp is enabled, the model is no longer minimizing “classification error” in the traditional sense.

It is minimizing a richer cost function that encodes smoothness, uncertainty, and robustness directly into the objective.

Once you understand the cost function, all the strange-looking training metrics stop being confusing — they become expected, explainable, and reassuring.

Config and Training Logs for Reference

========== CONFIG ==========
NUM_CLASSES = 10
TRAINING_SAMPLE_PER_CLASS = 100
VALIDATION_SAMPLE_PER_CLASS = 100
BATCH_SIZE = 256
EPOCHS = 60
TRAINABLE_LAYERS_STAGE1 = 1
TRAINABLE_LAYERS_STAGE2 = 2
EARLY_STOP_PATIENCE = 100
USE_COSINE_LR = True
COSINE_T_MAX = 60
COSINE_ETA_MIN = 1e-06
USE_MIXUP = True
MIXUP_ALPHA = 0.2
label smoothing = 0.15
============================

===== Stage-1: Train fc only =====
[01/60] Train Loss: 2.4538 | Val Loss: 2.4033 | Train Acc: 7.70% | Val Acc: 14.70%
[02/60] Train Loss: 2.2820 | Val Loss: 2.2168 | Train Acc: 11.40% | Val Acc: 22.00%
[03/60] Train Loss: 2.1846 | Val Loss: 2.0564 | Train Acc: 15.90% | Val Acc: 30.80%
[04/60] Train Loss: 2.1112 | Val Loss: 1.9382 | Train Acc: 24.20% | Val Acc: 36.40%
[05/60] Train Loss: 1.9790 | Val Loss: 1.8447 | Train Acc: 20.10% | Val Acc: 44.70%
[06/60] Train Loss: 1.8874 | Val Loss: 1.7559 | Train Acc: 42.90% | Val Acc: 52.20%
[07/60] Train Loss: 1.7439 | Val Loss: 1.6857 | Train Acc: 23.50% | Val Acc: 57.60%
[08/60] Train Loss: 1.7551 | Val Loss: 1.6398 | Train Acc: 8.80% | Val Acc: 59.00%
[09/60] Train Loss: 1.7286 | Val Loss: 1.6066 | Train Acc: 32.80% | Val Acc: 59.70%
[10/60] Train Loss: 1.6075 | Val Loss: 1.5637 | Train Acc: 36.80% | Val Acc: 62.00%
[11/60] Train Loss: 1.5552 | Val Loss: 1.5315 | Train Acc: 23.80% | Val Acc: 64.30%
[12/60] Train Loss: 1.5919 | Val Loss: 1.5085 | Train Acc: 42.60% | Val Acc: 64.90%
[13/60] Train Loss: 1.4833 | Val Loss: 1.4862 | Train Acc: 8.70% | Val Acc: 65.80%
[14/60] Train Loss: 1.7002 | Val Loss: 1.4808 | Train Acc: 41.70% | Val Acc: 64.90%
[15/60] Train Loss: 1.6000 | Val Loss: 1.4598 | Train Acc: 66.70% | Val Acc: 66.10%
[16/60] Train Loss: 1.5693 | Val Loss: 1.4629 | Train Acc: 48.40% | Val Acc: 64.90%
[17/60] Train Loss: 1.4862 | Val Loss: 1.4475 | Train Acc: 44.20% | Val Acc: 65.10%
[18/60] Train Loss: 1.6148 | Val Loss: 1.4369 | Train Acc: 45.70% | Val Acc: 65.70%
[19/60] Train Loss: 1.5109 | Val Loss: 1.4300 | Train Acc: 49.90% | Val Acc: 65.50%
[20/60] Train Loss: 1.4189 | Val Loss: 1.4157 | Train Acc: 45.10% | Val Acc: 67.00%
[21/60] Train Loss: 1.3092 | Val Loss: 1.4088 | Train Acc: 59.80% | Val Acc: 68.20%
[22/60] Train Loss: 1.3527 | Val Loss: 1.3958 | Train Acc: 44.80% | Val Acc: 67.80%
[23/60] Train Loss: 1.5931 | Val Loss: 1.3922 | Train Acc: 45.20% | Val Acc: 67.90%
[24/60] Train Loss: 1.7500 | Val Loss: 1.4134 | Train Acc: 23.80% | Val Acc: 65.10%
[25/60] Train Loss: 1.2768 | Val Loss: 1.3895 | Train Acc: 45.30% | Val Acc: 68.30%
[26/60] Train Loss: 1.4332 | Val Loss: 1.3798 | Train Acc: 32.90% | Val Acc: 68.60%
[27/60] Train Loss: 1.4859 | Val Loss: 1.3846 | Train Acc: 57.80% | Val Acc: 67.80%
[28/60] Train Loss: 1.5004 | Val Loss: 1.3907 | Train Acc: 37.80% | Val Acc: 66.60%
[29/60] Train Loss: 1.4174 | Val Loss: 1.3818 | Train Acc: 30.00% | Val Acc: 68.40%
[30/60] Train Loss: 1.5095 | Val Loss: 1.3813 | Train Acc: 38.90% | Val Acc: 68.50%
[31/60] Train Loss: 1.3503 | Val Loss: 1.3746 | Train Acc: 27.30% | Val Acc: 68.70%
[32/60] Train Loss: 1.4783 | Val Loss: 1.3773 | Train Acc: 24.30% | Val Acc: 67.50%
[33/60] Train Loss: 1.2495 | Val Loss: 1.3660 | Train Acc: 62.70% | Val Acc: 69.30%
[34/60] Train Loss: 1.2894 | Val Loss: 1.3594 | Train Acc: 46.90% | Val Acc: 69.80%
[35/60] Train Loss: 1.7056 | Val Loss: 1.3801 | Train Acc: 35.60% | Val Acc: 67.70%
[36/60] Train Loss: 1.2149 | Val Loss: 1.3682 | Train Acc: 28.60% | Val Acc: 68.80%
[37/60] Train Loss: 1.4249 | Val Loss: 1.3705 | Train Acc: 9.40% | Val Acc: 68.50%
[38/60] Train Loss: 1.3438 | Val Loss: 1.3629 | Train Acc: 10.90% | Val Acc: 69.20%
[39/60] Train Loss: 1.6903 | Val Loss: 1.3755 | Train Acc: 37.30% | Val Acc: 67.10%
[40/60] Train Loss: 1.5488 | Val Loss: 1.3800 | Train Acc: 38.00% | Val Acc: 67.10%
[41/60] Train Loss: 1.7011 | Val Loss: 1.3965 | Train Acc: 46.20% | Val Acc: 65.80%
[42/60] Train Loss: 1.4152 | Val Loss: 1.3931 | Train Acc: 34.40% | Val Acc: 66.00%
[43/60] Train Loss: 1.2278 | Val Loss: 1.3697 | Train Acc: 62.50% | Val Acc: 68.10%
[44/60] Train Loss: 1.2642 | Val Loss: 1.3602 | Train Acc: 44.20% | Val Acc: 69.60%
[45/60] Train Loss: 1.4752 | Val Loss: 1.3633 | Train Acc: 58.30% | Val Acc: 68.50%
[46/60] Train Loss: 1.3039 | Val Loss: 1.3590 | Train Acc: 25.40% | Val Acc: 69.10%
[47/60] Train Loss: 1.3993 | Val Loss: 1.3570 | Train Acc: 44.40% | Val Acc: 69.30%
[48/60] Train Loss: 1.6299 | Val Loss: 1.3690 | Train Acc: 27.20% | Val Acc: 68.30%
[49/60] Train Loss: 1.2138 | Val Loss: 1.3565 | Train Acc: 46.20% | Val Acc: 69.20%
[50/60] Train Loss: 1.2929 | Val Loss: 1.3551 | Train Acc: 43.60% | Val Acc: 69.30%
[51/60] Train Loss: 1.2729 | Val Loss: 1.3535 | Train Acc: 28.80% | Val Acc: 69.60%
[52/60] Train Loss: 1.3955 | Val Loss: 1.3553 | Train Acc: 60.20% | Val Acc: 69.60%
[53/60] Train Loss: 1.4541 | Val Loss: 1.3574 | Train Acc: 30.60% | Val Acc: 69.30%
[54/60] Train Loss: 1.6126 | Val Loss: 1.3681 | Train Acc: 33.90% | Val Acc: 68.10%
[55/60] Train Loss: 1.3494 | Val Loss: 1.3616 | Train Acc: 49.70% | Val Acc: 68.90%
[56/60] Train Loss: 1.5867 | Val Loss: 1.3702 | Train Acc: 24.10% | Val Acc: 68.20%
[57/60] Train Loss: 1.5149 | Val Loss: 1.3728 | Train Acc: 23.30% | Val Acc: 67.50%
[58/60] Train Loss: 1.3746 | Val Loss: 1.3648 | Train Acc: 20.70% | Val Acc: 68.60%
[59/60] Train Loss: 1.3136 | Val Loss: 1.3619 | Train Acc: 61.80% | Val Acc: 69.00%
[60/60] Train Loss: 1.3522 | Val Loss: 1.3619 | Train Acc: 40.40% | Val Acc: 68.70%

Stage-1 Best results:
Train Loss: 1.2894 | Val Loss: 1.3594 | Train Acc: 46.90% | Val Acc: 69.80%
Stage-1 Training Time: 237.97 seconds

Loaded Stage-1 best-val model for Stage-2 fine-tuning

===== Stage-2: Unfreeze layer4 + fc =====
[01/60] Train Loss: 1.4827 | Val Loss: 1.2912 | Train Acc: 26.20% | Val Acc: 75.10%
[02/60] Train Loss: 1.3821 | Val Loss: 1.2489 | Train Acc: 61.30% | Val Acc: 75.90%
[03/60] Train Loss: 0.9931 | Val Loss: 1.1952 | Train Acc: 53.70% | Val Acc: 78.50%
[04/60] Train Loss: 1.1753 | Val Loss: 1.1775 | Train Acc: 55.10% | Val Acc: 79.40%
[05/60] Train Loss: 1.3549 | Val Loss: 1.1648 | Train Acc: 53.70% | Val Acc: 80.00%
[06/60] Train Loss: 0.9620 | Val Loss: 1.1515 | Train Acc: 31.50% | Val Acc: 81.40%
[07/60] Train Loss: 1.4032 | Val Loss: 1.1609 | Train Acc: 61.90% | Val Acc: 81.80%
[08/60] Train Loss: 0.9119 | Val Loss: 1.1382 | Train Acc: 34.80% | Val Acc: 82.60%
[09/60] Train Loss: 1.1922 | Val Loss: 1.1221 | Train Acc: 71.40% | Val Acc: 83.60%
[10/60] Train Loss: 1.0643 | Val Loss: 1.1156 | Train Acc: 65.00% | Val Acc: 83.50%
[11/60] Train Loss: 1.1285 | Val Loss: 1.1183 | Train Acc: 74.00% | Val Acc: 82.90%
[12/60] Train Loss: 0.8916 | Val Loss: 1.1177 | Train Acc: 55.80% | Val Acc: 83.30%
[13/60] Train Loss: 0.9120 | Val Loss: 1.1151 | Train Acc: 32.70% | Val Acc: 83.40%
[14/60] Train Loss: 0.9319 | Val Loss: 1.1033 | Train Acc: 76.70% | Val Acc: 83.70%
[15/60] Train Loss: 1.2321 | Val Loss: 1.1142 | Train Acc: 76.50% | Val Acc: 84.00%
[16/60] Train Loss: 1.0334 | Val Loss: 1.1162 | Train Acc: 12.70% | Val Acc: 84.40%
[17/60] Train Loss: 0.8715 | Val Loss: 1.1090 | Train Acc: 29.60% | Val Acc: 84.70%
[18/60] Train Loss: 1.0083 | Val Loss: 1.1018 | Train Acc: 69.70% | Val Acc: 84.60%
[19/60] Train Loss: 1.3475 | Val Loss: 1.1144 | Train Acc: 36.50% | Val Acc: 84.60%
[20/60] Train Loss: 1.1397 | Val Loss: 1.1288 | Train Acc: 96.00% | Val Acc: 83.80%
[21/60] Train Loss: 1.0031 | Val Loss: 1.1196 | Train Acc: 36.20% | Val Acc: 84.30%
[22/60] Train Loss: 1.0184 | Val Loss: 1.1032 | Train Acc: 64.60% | Val Acc: 84.70%
[23/60] Train Loss: 0.7571 | Val Loss: 1.0852 | Train Acc: 31.90% | Val Acc: 85.80%
[24/60] Train Loss: 1.1125 | Val Loss: 1.0823 | Train Acc: 15.60% | Val Acc: 86.00%
[25/60] Train Loss: 1.0659 | Val Loss: 1.0955 | Train Acc: 55.50% | Val Acc: 85.90%
[26/60] Train Loss: 0.8838 | Val Loss: 1.1081 | Train Acc: 31.60% | Val Acc: 86.00%
[27/60] Train Loss: 1.1226 | Val Loss: 1.1139 | Train Acc: 31.90% | Val Acc: 85.20%
[28/60] Train Loss: 0.9673 | Val Loss: 1.0937 | Train Acc: 28.30% | Val Acc: 85.40%
[29/60] Train Loss: 0.9817 | Val Loss: 1.0816 | Train Acc: 53.70% | Val Acc: 85.80%
[30/60] Train Loss: 0.9001 | Val Loss: 1.0748 | Train Acc: 34.20% | Val Acc: 85.70%
[31/60] Train Loss: 0.9982 | Val Loss: 1.0776 | Train Acc: 71.70% | Val Acc: 85.80%
[32/60] Train Loss: 0.9805 | Val Loss: 1.0824 | Train Acc: 10.20% | Val Acc: 85.40%
[33/60] Train Loss: 1.2955 | Val Loss: 1.0990 | Train Acc: 26.60% | Val Acc: 84.60%
[34/60] Train Loss: 0.7292 | Val Loss: 1.0914 | Train Acc: 79.10% | Val Acc: 85.60%
[35/60] Train Loss: 0.8313 | Val Loss: 1.0843 | Train Acc: 79.70% | Val Acc: 85.70%
[36/60] Train Loss: 0.9503 | Val Loss: 1.0832 | Train Acc: 53.60% | Val Acc: 85.70%
[37/60] Train Loss: 0.7882 | Val Loss: 1.0816 | Train Acc: 31.20% | Val Acc: 86.00%
[38/60] Train Loss: 0.8548 | Val Loss: 1.0846 | Train Acc: 79.50% | Val Acc: 86.30%
[39/60] Train Loss: 0.7730 | Val Loss: 1.0826 | Train Acc: 54.50% | Val Acc: 86.00%
[40/60] Train Loss: 0.9668 | Val Loss: 1.0825 | Train Acc: 24.00% | Val Acc: 86.40%
[41/60] Train Loss: 0.9407 | Val Loss: 1.0825 | Train Acc: 57.80% | Val Acc: 86.50%
[42/60] Train Loss: 1.0486 | Val Loss: 1.0890 | Train Acc: 33.70% | Val Acc: 86.60%
[43/60] Train Loss: 0.9799 | Val Loss: 1.0948 | Train Acc: 56.70% | Val Acc: 86.20%
[44/60] Train Loss: 0.8374 | Val Loss: 1.0972 | Train Acc: 52.00% | Val Acc: 86.50%
[45/60] Train Loss: 0.8803 | Val Loss: 1.0970 | Train Acc: 33.70% | Val Acc: 86.40%
[46/60] Train Loss: 0.7920 | Val Loss: 1.0935 | Train Acc: 32.80% | Val Acc: 86.40%
[47/60] Train Loss: 1.0537 | Val Loss: 1.0947 | Train Acc: 53.30% | Val Acc: 86.20%
[48/60] Train Loss: 1.0856 | Val Loss: 1.0972 | Train Acc: 55.40% | Val Acc: 86.30%
[49/60] Train Loss: 1.0134 | Val Loss: 1.0964 | Train Acc: 75.10% | Val Acc: 86.30%
[50/60] Train Loss: 0.9977 | Val Loss: 1.0942 | Train Acc: 63.90% | Val Acc: 86.20%
[51/60] Train Loss: 0.9315 | Val Loss: 1.0927 | Train Acc: 79.00% | Val Acc: 86.70%
[52/60] Train Loss: 1.2048 | Val Loss: 1.0955 | Train Acc: 38.00% | Val Acc: 86.30%
[53/60] Train Loss: 1.1794 | Val Loss: 1.0998 | Train Acc: 94.10% | Val Acc: 86.00%
[54/60] Train Loss: 0.9701 | Val Loss: 1.0974 | Train Acc: 78.90% | Val Acc: 86.20%
[55/60] Train Loss: 1.1620 | Val Loss: 1.1006 | Train Acc: 91.70% | Val Acc: 85.90%
[56/60] Train Loss: 0.7646 | Val Loss: 1.0934 | Train Acc: 55.60% | Val Acc: 86.40%
[57/60] Train Loss: 0.8303 | Val Loss: 1.0914 | Train Acc: 76.50% | Val Acc: 86.40%
[58/60] Train Loss: 0.7479 | Val Loss: 1.0883 | Train Acc: 33.70% | Val Acc: 86.10%
[59/60] Train Loss: 0.8376 | Val Loss: 1.0877 | Train Acc: 55.80% | Val Acc: 86.10%
[60/60] Train Loss: 0.7773 | Val Loss: 1.0870 | Train Acc: 34.00% | Val Acc: 86.40%

Stage-2 Best results:
Train Loss: 0.9315 | Val Loss: 1.0927 | Train Acc: 79.00% | Val Acc: 86.70%
Stage-2 Training Time: 312.37 seconds

Any comments? Feel free to participate below in the Facebook comment section.