Spatial & Temporal Queries on a Planar Graph
Amazon Spatial and temporal queries on a planar graph are a family of long standing problems in graph and theory.Basically on a planar network, which
can be likened to a road network or world-wide Internet network, we want to
find, for example, the closest neighbor of a node.
Our team needs to do a survey
on different approaches to solve these problems and try to generalize the
approaches. The papers include the following:
- [SKS02] C.Shahabi and M.R.K.M. Sharifzadeh. A road network embedding technique for k-nearest neighbor search in moving object databases. In ACM-GIS 2002, McLean, VA.
- [PZMT03] D.Papadias, J.Zhang, N.Mamoulis, and Y.Tao. Query Processing in Spatial Network Databases. In VLDB 2003, Berlin, Germany.
- [JKPT03] C. S. Jensen and J. Kolarvr and T. B. Pedersen and I. Timko. Nearest Neighbor Queries in Road Networks. In ACMGIS 2003, New Orleans, Louisiana, USA.
- [KS04] M. Kolahdouzan and C. Shahabi. Voronoi-based K Nearest Neighbor Search for Spatial Network Databases. In VLDB 2004, Toronto, Canada.
- [OBSC00] A. Okabe and B. Boots and K. Sugihara and S. N. Chiu. Spatial Tessellations, Concepts and Applications of Voronoi Diagrams. John Wiley and Sons Ltd., 2nd edition, 2000.
- [GKR04] S. Gupta and S. Kopparty and C. Ravishankar. 'Roads, Codes, and Spatiotemporal Queries', In PODS 2004, Paris, France.
Anyway, it all comes down to given a set of binary codes of the same length, given another binary codes of the same length find the one that has the smallest hamming distance to it. For example if your structure has:
10110
00000
11111
11110
01111
And your query is '01110', then you should give '01111' as the result since it is closest to '01110' hammingly. Obviously you can do this by storing the codes in a linear structure and simply going through them linearly for the answer (commonly known as the brute force way), but a better, faster approach should exist. It is what I call a 'Hamming tree' since to my knowledge nobody has beat me to it yet. You build a tree in which each pair of nodes that shares a tree edge has a Hamming distance of 1. There is more to it than that, but I wouldn't want to stifle you with all the details. Of course you are always welcome to ask me if you have questions.
The following is a table showing the performance of my Hamming tree against the brute force (Each code has 20 bits. Running time results are expressed in seconds):
| Number of codes | 10,000 | 50,000 | 100,000 |
| Brute Force k=1 k=20 k=50 |
.0299 .0599 .07 |
.1 .1899 .2599 |
.0599 .3199 .4099 |
| Hamming Tree k=1 k=20 k=50 |
0 .0599 .25 |
0 .0099 .0799 |
0 .0099 .0799 |
As you can see when the number of nodes is very high, Hamming Tree does a lot better than brute force. However, from a practical point of view the code size grows as O(square root of n), where n is the number of nodes.
Therefore a code
usually has a lot more than 20 bits, in which case building a Hamming tree takes
too long.
Anyway, it is a starting point for more serious research in this area
because my hunch just tells me that a better way than brute force almost always
exists!
Enjoy the following random pages..
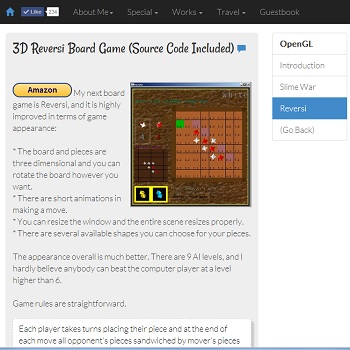 This website is Michael's official homepage.
This website is Michael's official homepage.
 This website is for Jeantour, a travel agency in Taipei, Taiwan.
This website is for Jeantour, a travel agency in Taipei, Taiwan.
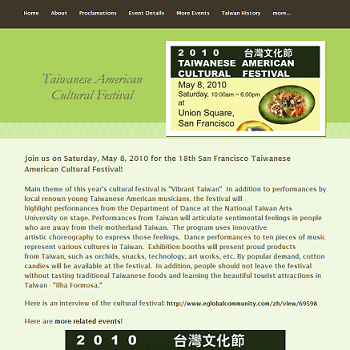 This website is for San Francisco Taiwanese American Festival held annually.
This website is for San Francisco Taiwanese American Festival held annually.
 This website is for a Taiwanese company who produces quality end mills and cutters.
This website is for a Taiwanese company who produces quality end mills and cutters.