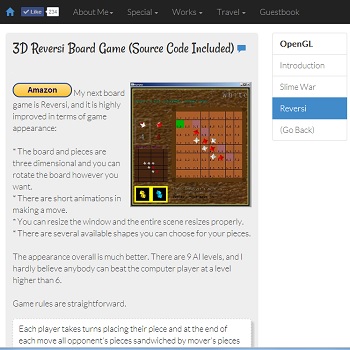
Michael's Interest in Parallel Computing
Amazon Parallel computing is also a huge research area. The idea is that multiple processors are used in solving a big problem so that it can be solved faster.Apparently if our current processor were fast enough, we probably wouldn't need parallel computing. Unfortunately the world is made to be challenging and interesting.
When you think about it you may feel parallel computing is simple to implement because conceptually, all you do is split up a big problem into a bunch of smaller ones and solve them in parallel and compose them into the solution to the original problem. That's what I thought initially, but it turns out that it's only partially true.
It's true that many problems can be statically decomposed into many small ones which can be solved quickly, but it's also true that many problems cannot be decomposed this way. Many problems use algorithms that are what we call recursion-based and you don't know in advance how to split them up.
A famous example is IBM's Deep Blue
Supercomputer that beat world's chess champion, Garry Kasparov. The machine
calculated all possible moves in parallel (thus gaining a huge speedup) and used
several metrics to get the move with the highest value.
The course in Java RMI has taught me a lot in distributed and parallel computing and I've
read many papers on parallel system implementations, including JavaSpaces,
JavaSymphony, Javalin, Cilk, Cx, Jicos, Jini, and Ibis. I just find it riveting. Our project, Document Search Engine,
is built on distributed and parallel concepts.
Take a look!